Die Rendite einer Kapitalanlage ist eine der wichtigsten Finanzkennzahlen. Für die Renditeberechnung benutzen wir beispielhaft die Dax-Kurse im Zeitraum 2013 bis 2017. Wie du diese oder andere externe Daten in importierst, erfährst du in meinem Beitrag So importierst du Daten in Excel. Es gibt zwei verschiedene Berechnungsmethoden, um eine Rendite zu berechnen: Die diskrete Rendite und die stetige Rendite.
Formel: Diskrete Rendite
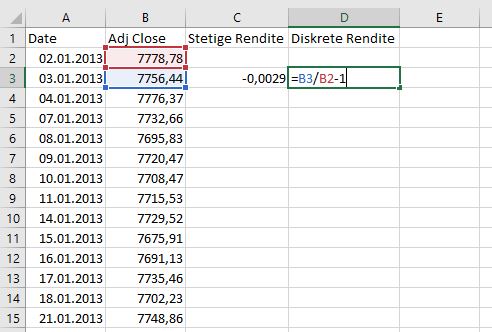
Diskrete Rendite: Rt = (Pt – Pt-1) / Pt-1 = Pt / Pt-1 – 1
mit:
| Pt | Kurs zum Zeitpunkt t |
| Pt-1 | Kurs zum Zeitpunkt t-1 |
Der Vorteil bei der diskreten Rendite besteht darin, dass die Rendite eines Portfolios die gewichtete Summe der Renditen der im Portfolio enthaltenen Wertpapiere ist. Die diskrete Rendite wird also vor allem bei Portfoliobetrachtungen verwendet.
Formel: Stetige Rendite
Stetige Rendite: rt = ln(Pt / Pt-1)
mit:
| Pt | Kurs zum Zeitpunkt t |
| Pt-1 | Kurs zum Zeitpunkt t-1 |
| ln() | natürlicher Logarithmus |
Stetige Renditen sind additiv entlang der Zeitachsen. Oft werden stetige Renditen auch als kontinuierliche Renditen bezeichnet, da diese Renditeberechnung eine kontinuierliche Verzinsung zwischen Anfangs- und Endwert beschreibt. Ein Nachteil besteht allerdings darin, dass die stetigen Renditen eines Portfolios nicht einfach die gewichtete Summe der Renditen der im Portfolio enthaltenen Wertpapiere sind. Die stetige Rendite wird für vor allem für Zeitreihenbetrachtungen und deren statistische Eigenschaften verwendet.

Umrechnung von stetiger zu diskreter Rendite
Mit dieser Formel kann man beide Renditearten umrechnen:
Umrechnung: Rt = ert – 1 und rt = ln(Rt + 1)
So berechnest du den Mittelwert von Renditen
Wenden wir beide Renditeberechnungen auf unsere Dax-Daten an. Der Mittelwert bzw. das arithmetische Mittel wird in Excel mittels der Funktion =MITTELWERT() gebildet. Wir wenden die Funktion auf beide berechneten täglichen Renditen an.
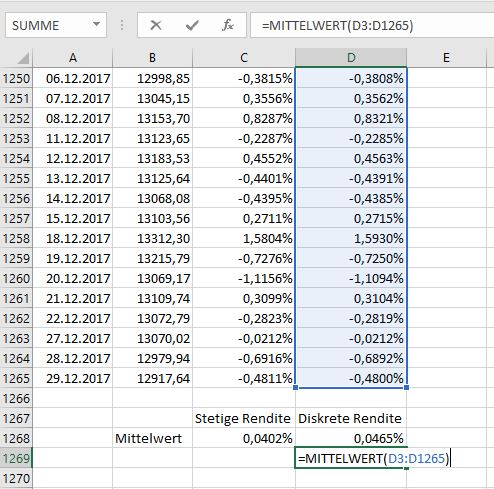
Hier zeigt sich eine deutliche Abweichung beider Werte (Stetig: 0,0402% vs. Diskret: 0,0465%). Je größer die Schwankungen der Renditen, desto größer ist die Abweichung von stetiger und diskreter Rendite. In diesem Fall ist der Mittelwert der stetigen Rendite der korrekte Wert.
Wie hoch ist die Rendite über den kompletten Zeitraum?
Um zu erfahren, was eine Anlage in den Dax am 02.01.2013 bis zum 29.12.2017 gebracht hätte, berechnen wir nun die Rendite über den kompletten Zeitraum (5 Jahre). Da die stetige Rendite additiv ist, kann zunächst die Summe über alle Renditen genommen werden. Diese Summe wird nun in folgender Formel verwendet.
Rendite 5J = e∑ – 1
Die e-Funktion (Exponentialfunktion) erzielt man in Excel mittels =EXP().

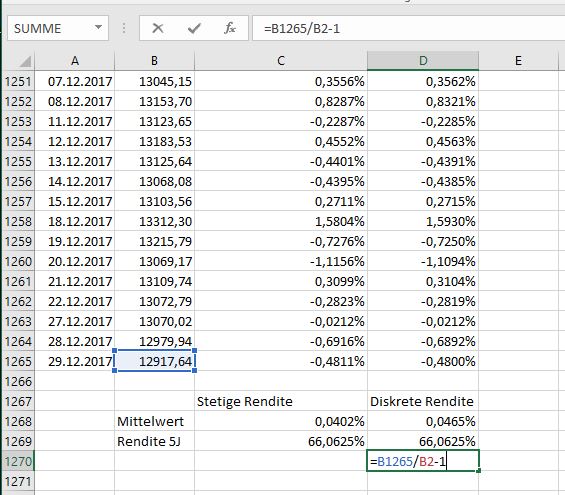
Bei der diskreten Rendite geht das ganze etwas einfacher. Hier teilen wir lediglich den End- durch den Startwert und ziehen die Zahl 1 ab. In beiden Fällen erhalten wir eine Rendite für den kompletten Zeitraum von 66,0625%.
Exkurs: Wöchentliche, monatliche und jährliche Renditen berechnen
Sollte es nicht möglich sein, entsprechende Daten von einer Datenbank oder externen Quelle in einem anderen Zeitformat zu beziehen, so können wir mit ein paar Hilfsmitteln auch selbst diese Renditen berechnen. Der Einfachheit kopiere ich die Spalte „Date“ und den adjustierten Schlusskurs („Adj Close“) in ein neues Blatt.
Mithilfe der Funktion =WOCHENTAG(„Zelle“;2) lassen sich die Daten mit dem jeweiligen Wochentag markieren. Dabei steht in dieser Einstellung die 1 für den Montag und die 5 für den Freitag.
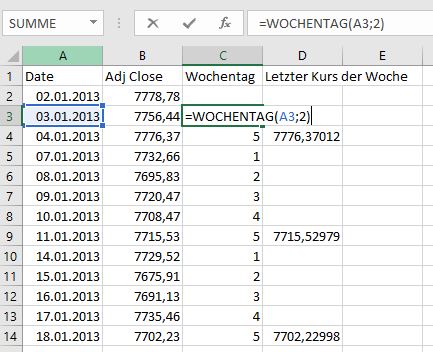
Da aufgrund von Feiertagen nicht zwangsweise der Freitag der letzte Handelstag in der Woche sein muss, lasse ich mir in der Spalte D den jeweils letzten Kurs der Woche abtragen, sofern die Zahl in Spalte C größer ist als der nächste Tag. Ansonsten soll nicht angezeigt werden.

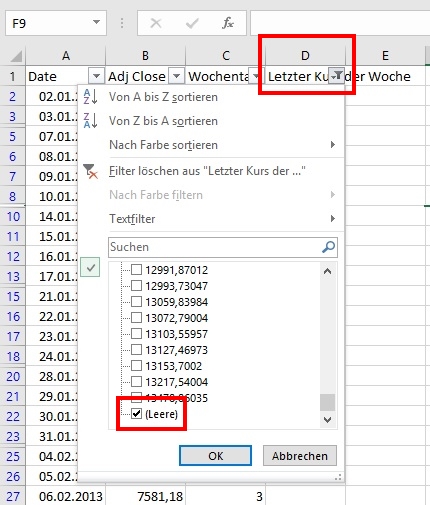
Anschließend sortiere ich (STRG+SHIFT+L) die Daten und wähle alle leeren Zellen in Spalte D aus. Diese werden alle gelöscht. Damit bleiben nur noch die letzten Kurse der Woche übrig. Die Hilfsspalten C und D können ebenfalls gelöscht werden. Nun kann wieder mittels ln-Funktion die stetige Rendite rt = ln(Pt / Pt-1) auf wöchentlicher Basis berechnet werden.
Achtung, bei der monatsweisen Betrachtung mithilfe der Excel-Funktion =MONAT() gibt es eine Feinheit zu beachten: Beim Jahreswechsel ist der folgende Monat (1 für Januar) von der Zahl kleiner als der vergangene Monat (12 für Dezember). Abhilfe schafft folgende Bedingung:

Mit dieser Formel erhalten wir alle Dax-Kurse zum jeweiligen Monatswechsel – sogar wenn Januar auf Dezember folgt. Auch hier können wieder mittels Sortierung die leeren Zellen in Spalte D gelöscht werden sowie anschließend die Hilfsspalte C. Mit den übrig gebliebenen Daten werden können nun Renditen auf monatlicher Basis berechnet werden.
Für Renditen auf Jahresbasis verwende die Excel-Funktion =JAHR(). Die Wenn-Funktion ist nahezu identisch mit der Berechnung für wöchentliche Renditen. Die kleine Änderung ist =WENN(C4<C5;B4;““).