Du bist auf den Begriff CAGR gestoßen und möchtest wissen, wie man ihn in Excel berechnet? Dieser Beitrag bietet dir vier verschiedene Möglichkeiten, dies in Microsoft Excel zu tun. Aber zuerst wollen wir verstehen, was CAGR eigentlich ist.
Was ist CAGR?
Unter CAGR versteht man die durchschnittliche jährliche Wachstumsrate. Die Abkürzung CAGR steht für Compound Annual Growth Rate. Ganz einfach gesagt, bezeichnet man damit die Geschwindigkeit, mit der etwas über einen Zeitraum von Jahren wächst, unter Berücksichtigung der Wirkung des Zinseszinseffekts. Beispielsweise die Rendite einer Investition über einen bestimmten Zeitraum, ausgedrückt in Jahresprozenten.
Bedenke, dass der CAGR mehr oder weniger ein imaginärer Begriff ist. Der CAGR dient dir lediglich als Indikator, der dir sagt, wie bspw. die Dividende im Laufe der Zeit gewachsen ist. Und das unter der Voraussetzung eines konstanten Zinssatzes bzw. einer konstanten Wachstumsrate.
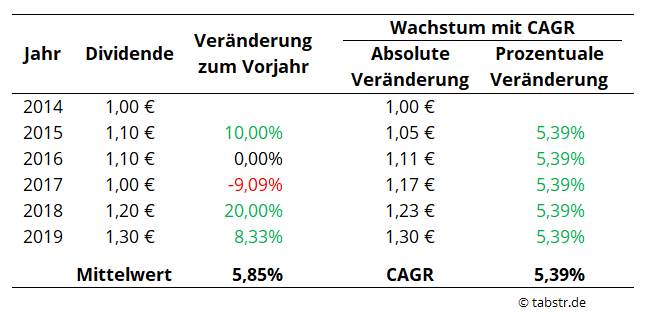
Dieses Beispiel zeigt dir die absolute Entwicklung einer hypothetischen Dividendenzahlung in den Jahren 2014 bis 2019. Die Prozentzahlen in „Veränderung zum Vorjahr“ werden als ganz normale Wertveränderung berechnet. Du erkennst sicher gut, dass die tatsächlichen Wachstumsraten für jedes Jahr unterschiedlich sind. Der Mittelwert dieser prozentualen Veränderungen entspricht 5,85%. Mit diesem Wert weitere Berechnungen auf die künftige Steigerung der Dividendenzahlungen anzustellen wäre aber unter Umständen falsch.
Denn die tatsächliche jährliche Steigerung hat laut CAGR nur 5,39% betragen.
Auch gleichbleibende und sogar negative Wachstumsraten sind in der Realität möglich. Die CAGR-Wachstumsrate betrachtet aber lediglich den Start- und Endwert sowie die Anzahl der Perioden.
Die CAGR Formel
Die CAGR Formel erfordert nur drei Eingaben: den Anfangswert einer Investition, den Endwert und die Anzahl der Perioden (ausgedrückt in Jahren). Falls du die ganz normale Wertentwicklung errechnen willst, dass kann ich dir meinen Beitrag Rendite in Excel berechnen empfehlen.
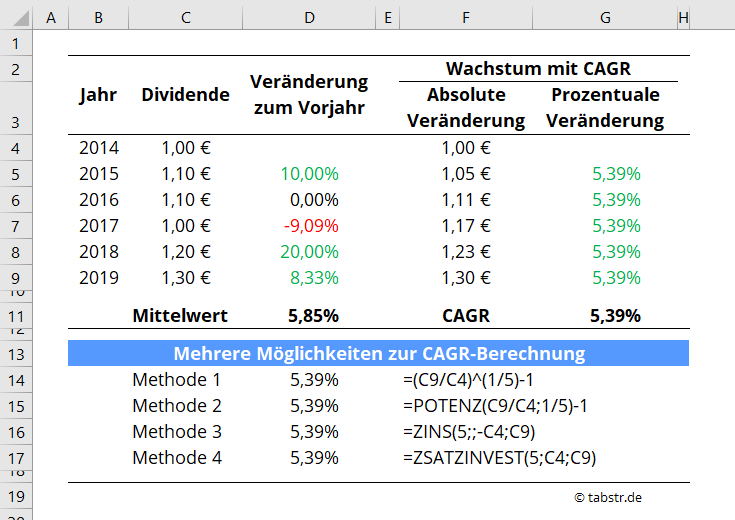
Ich stelle dir nachfolgend vier verschiedene Methoden vor, um den CAGR zu berechnen.
Methode 1: CAGR direkt per Hand in Excel berechnen
Bevor wir in Excel eintauchen, sehen wir uns die Berechnung der durchschnittlichen jährlichen Wachstumsrate genauer an. Die Formel lautet:
Beachte, dass die Anzahl der Perioden immer die Anzahl der Veränderungen darstellt. In unserem Beispiel mit der Dividende sind es folglich 5 Perioden.
- Periode 1: 2014 –> 2015
- Periode 2: 2015 –> 2016
- Periode 3: 2016 –> 2017
- Periode 4: 2017 –> 2018
- Periode 5: 2018 –> 2019
In Excel kannst du das ganz leicht mit der Formel =ANZAHL(Erstes Jahr : Letztes Jahr) – 1 lösen.
Methode 2: CAGR mit der Potenz-Funktion in Excel berechnen
Anstatt die Formel aus Methode 1 manuell einzutippen, kannst du auch die Potenz-Funktion in Excel verwenden, um den CAGR zu berechnen. Das Ergebnis ist natürlich das gleiche, aber es lässt die Formel etwas sauberer aussehen. Ich persönlich verwende aber immer Methode 1. Noch einfacher geht es allerdings mit Methode 4.
Für das Dividenden-Beispiel wäre die Berechnung wie folgt:
Die Formel ersetzt im Grunde nur das Potenzzeichen ^ aus Methode 1.
Methode 3: CAGR mit der Zins-Funktion in Excel berechnen
Eine weitere, aber viel weniger verbreitete Methode ist es, den CAGR mit der Zins-Funktion in Excel zu berechnen. Diese Art der Berechnung ist noch sauberer als Methode 2. Obwohl die Formel kompliziert aussieht, brauchst du nur drei Variablen einzusetzen.
Mit
- Zzr: Anzahl der Perioden (hier: 5)
- Rmz: Nichts eintragen
- Bw: Der Startwert mit einem Minus davor (hier: -1,00)
- Zw: Der Endwert (hier: 1,30)
- F: Nichts eintragen
- Schätzwert: Nichts eintragen
Möchtest du es noch komfortabler haben, dann sieh dir direkt Methode 4 an.
Methode 4: Mein Tipp – CAGR mit der Zsatzinvest-Funktion in Excel berechnen
Noch deutlich einfacher und vor allem weniger fehleranfällig ist die CAGR-Berechnung mit der Excel-Formel =ZSATZINVEST(). Trage hier nur in dieser Reihenfolge die Anzahl der Perioden, den Startwert und den Endwert ein. Fertig.
Einfacher geht es nicht. Bei dieser Methode musst du nicht darauf achten ein Minus vor den Startwert zu setzen, oder dir merken, welche Variable frei gelassen werden muss wie in Methode 3.
CAGR mit negativen Werten berechnen – was geht und was nicht
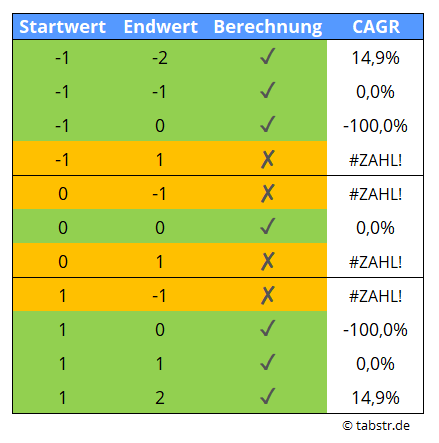
Die bisher verwendeten Beispiele haben sich stets mit positiven Zahlen beschäftigt. Kommen negativen Zahlen ins Spiel kann es sein, dass die CAGR-Formel nicht mehr funktioniert. Nachfolgend findest du verschiedene Fälle. Die CAGR-Berechnungen wurden mit fünf Perioden erstellt.
Sowohl beim Start, als auch beim Endwert sind positive und negative Werte sowie die Null denkbar. In vier Fällen liefert die Zsatzinvest-Formel eine Fehlermeldung.
CAGR mit genauen Datumswerten: Unterjährige Entwicklung exakt berechnen
In der Realität fallen allerdings Zahlungsströme wie Dividenden nicht immer am exakt gleichen Tag an. Auch wenn du bspw. eine Aktie kaufst und wieder verkaufst wird das mit hoher Wahrscheinlichkeit nicht immer in genauen Jahresabständen der Fall sein. Falls du hier aber einen genauen CAGR berechnen willst, dann habe ich auch für diesen Fall eine Lösung.
Der Trick, den CAGR mit genauen Datumswerten in Excel zu berechnen, besteht darin den richtigen Wert für die Anzahl der Perioden zu verwenden.
In diesem Beispiel erfolgte der Kauf einer Aktie am 12.05.2014 für einen Preis von 100 Euro. Der Verkauf erfolgte fünf Jahre später am 24.05.2019 zu 130 Euro. Die Differenz der Jahre kann man in der Regel noch leicht im Kopf berechnen – bei der genauen Anzahl der Tage wird dies schon schwieriger. Aber dafür hat Excel eine Formel parat. Mit der Excel-Formel Datedif kannst du dir die Anzahl der Tage, Monate oder Jahre zwischen zwei Datumsangaben berechnen.
Verwende für das Start- und Enddatum die tatsächlichen Datumswerte. Mit „Format“ kannst du bestimmen, welche Differenz gebildet werden soll. Denkbar sind folgende Möglichkeiten:
- „Y“: Year – Die Anzahl der vollständigen Jahre im Zeitraum
- „M“: Month – Die Anzahl der vollständigen Monate im Zeitraum
- „D“: Day – Die Anzahl der Tage im Zeitraum
- „MD“: Month-Date – Die Differenz zwischen den Tagen in „Startdatum“ und „Enddatum“. Die Monate und Jahre der Datumsangaben werden ignoriert.
- „YM“: Year-Month – Die Differenz zwischen den Monaten in „Ausgangsdatum“ und „Enddatum“. Die Tage und Jahre der Datumsangaben werden ignoriert.
- „YD“: Year-Date – Die Differenz zwischen den Tagen in „Startdatum“ und „Enddatum“. Die Jahre der Datumsangaben werden ignoriert.
Für den CAGR benötigst du nur die Differenz der ganzzahligen Jahre „Y“ und die verbleibenden Tage „YD“. Die Anzahl der verbleibenden Tage teilst du durch 365 und erhält somit den Bruchteil eines ganzen Jahres. Addiere nun die Anzahl der ganzen Jahre und den einen Bruchteil (hier: 5+0,0329=5,0329 Perioden).
Diese Zahl mit den Nachkommastellen verwendest du für die Anzahl der Perioden. Jetzt kannst du den genauen unterjährigen CAGR in Excel berechnen. Das funktioniert mit allen vier Methoden. Der CAGR für 5 Jahre und 12 Tage beträgt in diesem Beispiel 5,35% mit der Berechnung = ZSATZINVEST(100;130;5,0329).
Beispiele zur CAGR Berechnung
Damit du besser verstehst, wie die durchschnittliche Wachstumsrate berechnet wird, habe ich dir fünf Beispiele erstellt. Das Beste: Alle CAGR Beispiele stehen dir als Excel Download kostenfrei zur Verfügung!
Beispiel 1: Mittlere Wachstumsrate der Weltbevölkerung
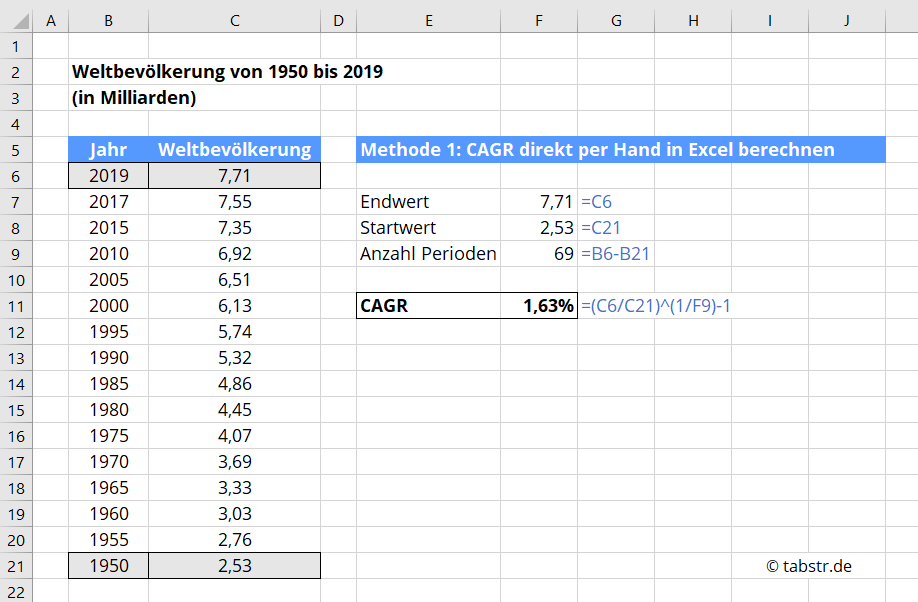
Das erste Beispiel ist sehr interessant. Die Weltbevölkerung der Erde lag im Jahre 1950 noch bei 2,53 Milliarden Menschen. Im Jahre 2019 sind es bereits 7,71 Milliarden Menschen.
Wie hoch war nun das durchschnittliche Wachstum der Weltbevölkerung?
Dieses Beispiel zeige ich dir mit Methode 1 der CAGR Berechnung.
Du kannst diese Formel direkt in Excel einfügen und erhältst die korrekte Wachstumsrate.
=(7,71/2,53)^(1/69)
Das Ergebnis lautet 1,63%. Jedes Jahr wächst die Weltbevölkerung also um 1,63%.
Beispiel 2: Durchschnittliche Steigerung der Dividendenzahlungen der DAX Unternehmen
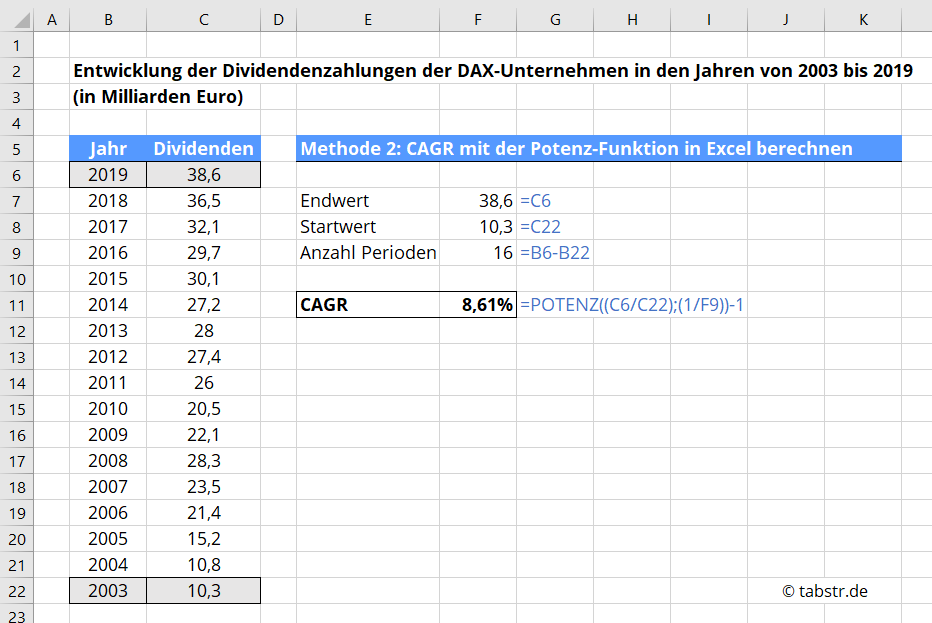
Vor allem Finanzkennzahlen werden oft als CAGR berechnet. Ein klasse Beispiel hierfür sind Dividendenzahlungen. Nachfolgend siehst du die Entwicklung der Dividendenzahlungen der DAX-Unternehmen von 2003 bis 2019. Beginnend mit 10,3 Milliarden Euro in 2003 stiegen die Dividendenzahlungen auf 38,6 Milliarden Euro in 2019.
Wie hoch war nun die durchschnittliche Steigerung der Dividendenzahlungen?
Für dieses Beispiel verwende ich Methode 2 der CAGR Berechnung.
Du kannst diese Formel direkt in Excel einfügen und erhältst den korrekten CAGR Wert.
=POTENZ((38,6/10,3);(1/16))-1
In diesem Beispiel beträgt das durchschnittliche jährliche Wachstum der Dividendenzahlungen 8,61%. Für einen Investor ist das eine wichtige Erkenntnis. Denn mit der Kennzahl können mehrere Anlagen verglichen werden, da sie auf einer jährlichen Basis normiert ist.
Beachte: Die Höhe der Zahlungen von 2004 bis 2018 werden beim CAGR ignoriert. Extreme Schwankungen innerhalb dieses Zeitraums könnten also von der tatsächlichen Entwicklung einen falschen Eindruck vermitteln. Ein besseres Beispiel zeige ich dir in CAGR Nachteile.
Beispiel 3: Wachstum durchschnittlicher Brutto-Arbeitslohn
Ein weiteres spannendes Beispiel ist die Entwicklung der Durchschnittseinkommen. Das Durchschnittseinkommen wird hier als Brutto-Jahresarbeitslohn je ledigem Arbeitnehmer ohne Kinder angegeben.
Im Jahr 2000 betrug das durchschnittliche Einkommen noch 25.479 €, wohingegen es im Jahr 2018 um knapp 10.000 € angestiegen ist.
Um wie viel ist aber das Durchschnittseinkommen in Prozent pro Jahr gestiegen?
Dieses Beispiel zeige ich dir mit Methode 3 zur Berechnung der stetigen Wachstumsrate.
Du kannst diese Formel direkt in Excel einfügen und erhältst den korrekten CAGR Wert.
=ZINS(18;;-25479;35189)
Beachte das Minuszeichen beim Startwert!
Das Ergebnis ist 1,81%. Wie ist dieser CAGR Wert zu interpretieren? Der durchschnittliche Brutto-Jahresarbeitslohn steigt seit 2000 jedes Jahr um durchschnittlich 1,81% an. Das sind wenige Prozentpunkte mehr als die durchschnittliche Inflation. Das bedeutet, dass im Durchschnitt auch weiterhin Güter und Dienstleistungen bezahlt werden können. Allerdings fehlen bei dieser Betrachtung viele weitere Einflussfaktoren.
Welchen dramatischen Einfluss die Inflation langfristig hat und wie du die Inflation berechnest, zeige ich dir in meinem Beitrag Geldvernichter Inflation.
Beispiel 4: Wachstumsrate Bruttoinlandsprodukt (BIP) Deutschland
Ein weiteres klassisches Szenario ist die Ermittlung der durchschnittlichen Wachstumsrate des Bruttoinlandsprodukts. Im Jahr 2000 betrug die Wirtschaftsleistung Deutschlands noch 2,1 Billionen Euro. Bereits 2019 beträgt das Bruttoinlandsprodukt 3,4 Billionen Euro.
Die klassische Frage würde lauten: Wie hoch ist die jährliche Wachstumsrate des BIPs in Deutschland?
Für dieses Beispiel verwende ich Methode 4 der CAGR Berechnung. Das ist meines Erachtens die leichteste CAGR-Formel. Du benötigst nur die Anzahl der Perioden, den Start- und Endwert.
Du kannst die ZSATZINVEST-Formel direkt in Excel einfügen und erhältst die richtige durchschnittliche Wachstumsrate.
=ZSATZINVEST(19;2109,1;3436,0)
Mit der Formel erhalten wir eine durchschnittlich jährliche Steigerung des BIPs von 2,60%.
Beispiel 5: Mit genauen Datumswerten den CAGR deines Portfolios berechnen
Sehr oft soll auch der jährliche Wachstumswert eines Wertpapierportfolios berechnet werden. Meist hast du zu einem speziellen Datum den Ausgangswert des Portfolios gegeben und sollst für ein späteres Datum dann die Compound Annual Growth Rate bestimmen. Das kannst du ganz leicht in Excel rechnen.
Das Problem: Mit einem genauen Datum hast du keine gerade Anzahl an Perioden.
Du musst also zuallererst die genaue Anzahl an Perioden ermitteln.
Das geht mit den Formeln =DATEDIF(Startdatum;Enddatum;”Y”) für die Anzahl der kompletten Jahre.
Außerdem benötigst du noch mittels =DATEDIF(Startdatum;Enddatum;”YD”) die Anzahl der verbleibenden Tage. Teile dieses Wert durch 365, um die Tage in Jahre zu konvertieren. Addiere diesen Wert dann zu der Anzahl der kompletten Jahre.
Als nächsten Schritt kannst du eine CAGR-Formel deiner Wahl verwenden. Ich habe in diesem Beispiel Methode 1 und 4 verwendet.
Als richtige Wachstumsrate erhältst du 9,02%. Würdest du nicht mit den genauen Datumsangaben rechnen, dann würdest du einen Wert von 9,14% erhalten und somit den wahren Werten überschätzen.
Bonus: Mit dem CAGR einen Wert in der Zukunft vorhersagen (CAGR Forecast)
Du kannst mit der mittleren Wachstumsrate auch einen Forecast anstellen. Dazu berechnest du zuerst den CAGR von einer bestehenden Zeitreihe. Anschließend wird die Wachstumsrate verwendet, um die Zeitreihe in die Zukunft weiterzurechnen.
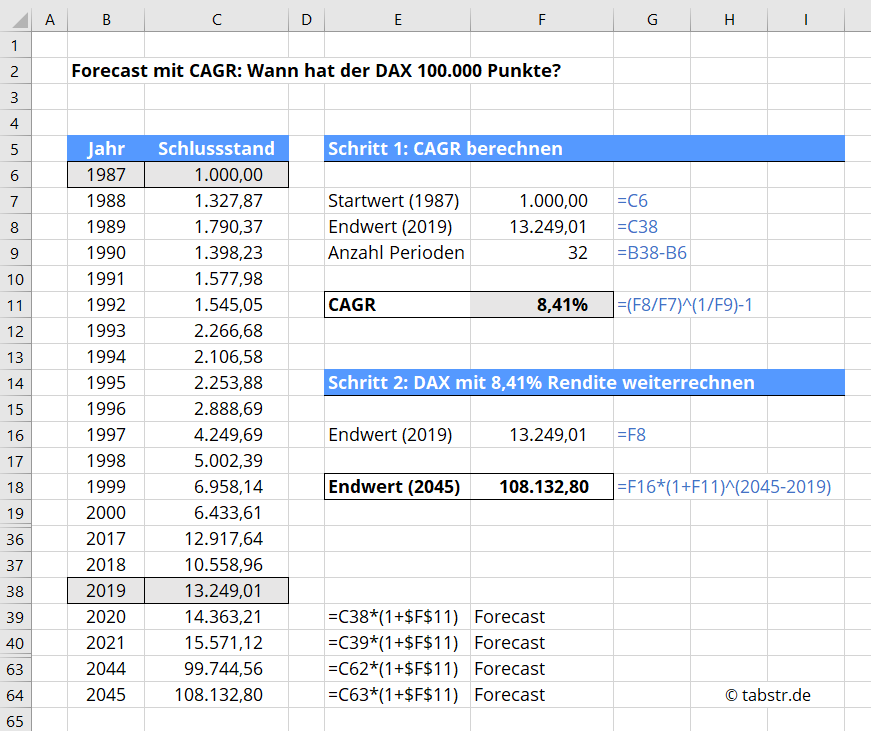
Ein gutes Beispiel wäre etwa: Wann steht der DAX bei 100.000 Punkten?
Der Deutsche Aktienindex (DAX) startete 1987 bei 1.000 Punkten. Im Jahr 2019 hatte er einen Endstand von 13.249 Punkten. Bei 32 Jahren ergibt sich ein CAGR von 8,41%. Der DAX ist also durchschnittlich jedes Jahr um 8,41% gestiegen.
Die Formel zum direkt in Excel einfügen lautet:
=(13249,01/1000)^(1/32)
Als nächstes müssen die zukünftigen Jahre berechnet werden. Der Jahresendstand von 2019 wird jetzt mit den 8,41% aufgezinst.
Das kannst du mit der folgenden Formel berechnen:
=13249,01*(1+8,41%)
Das Ergebnis von 14.363,21 ist der Schlussstand im Jahr 2020. Führe jetzt wieder eine Aufzinsung um 8,41% durch.
Im Jahre 2045 wird der DAX dann erstmals die Marke von 100.000 Punkten überschreiten.
Du könntest als weiteres Beispiel berechnen, in welchem Jahr es mehr als 10 Milliarden Menschen auf der Welt gibt. Siehe dazu Beispiel 1.
Download: Beispiele zur CAGR Berechnung
Ich habe dir alle 5 Beispiele und den Forecast in einer Excel zusammengefasst. Du kannst die Datei downloaden, um die genauen Rechenwege zu verfolgen.
Online CAGR Rechner: Berechne die durchschnittliche Wachstumsrate
Du möchtest schnell den CAGR online berechnen? Dann nutze dafür einfach den nachfolgenden Rechner. Ich habe dir beide Varianten zur Verfügung gestellt. Einmal mit ganzzahligen Perioden bzw. Jahren und einmal mit genauen Datumsangaben.
In die gelben Felder kannst du deine eigenen Werte eintragen. Der CAGR wird dann automatisch berechnet. Viel Spaß damit!
Die CAGR Formel umstellen
Wie jede mathematische Formel kannst du auch die CAGR Formel umstellen. So kannst du den Startwert, Endwert oder die Anzahl der benötigten Perioden berechnen.
Ich habe dir für alle drei Varianten ebenfalls einen online CAGR Rechner erstellt. In Variante 1 kannst du bei gegebener Wachstumsrate, Endwert und Anzahl der Perioden den Startwert berechnen.
Möchtest du lediglich den Endwert berechnen, so musst du in Variante 2 nur den Startwert, CAGR und die Anzahl der Perioden eingeben.
In Variante 3 wird dir die Anzahl der benötigten Perioden ausgegeben.
Viel Spaß beim Testen!
CAGR Vorteile
Der CAGR ist dem Mittelwert (einfaches arithmetisches Mittel) überlegen, da er den Zinseszinseffekt berücksichtigt.
CAGR Nachteile
Der CAGR dämpft die Wahrnehmung der Volatilität. Für die Berechnung werden nur Start- und Endwert sowie die Anzahl der Perioden betrachtet. Nicht aber was innerhalb der Perioden passiert. Dazu ein Beispiel mit einem Startwert von 100:
| Periode | Wertveränderung | Wert |
|---|---|---|
| 0 | 100 | |
| 1 | -50% | 50 |
| 2 | +100% | 100 |
| 3 | +10% | 110 |
In diesem Beispiel wäre es ein 3,23% CAGR, aber die Volatilität der Renditen ist enorm. Würde man nur einen Blick auf den CAGR werfen, so würde man einen irreführenden Eindruck von der tatsächlichen Entwicklung vermittelt bekommen. Die CAGR-Berechnung in diesem Beispiel ist (110/100)^(1/3) – 1 = 3,23%.
Quellen:
- Beispiel 1: https://www.un.org/en/development/desa/population/index.asp
- Beispiel 2: https://de.statista.com/statistik/daten/studie/4761/umfrage/dividendenzahlungen-der-dax-unternehmen/
- Beispiel 3: https://de.statista.com/statistik/daten/studie/164047/umfrage/jahresarbeitslohn-in-deutschland-seit-1960/
- Beispiel 4: https://www.destatis.de/DE/Themen/Wirtschaft/Volkswirtschaftliche-Gesamtrechnungen-Inlandsprodukt/Tabellen/bip-bubbles.html
- Beispiel 5: https://de.wikipedia.org/wiki/DAX#J%C3%A4hrliche_Entwicklung